Almost every field in ML has been affected by the advance of LLMs, and while there are constant improvements in all the free and commercial models, they follow a similar process for generating their results. Diffusion large language models (dLLM) are a new paradigm for token generation that is promising enough to be considered as a new approach for building large language models that can be cheaper and potentially better for tasks like code generation. Let’s have a look at the diffusion large language models and how they work.
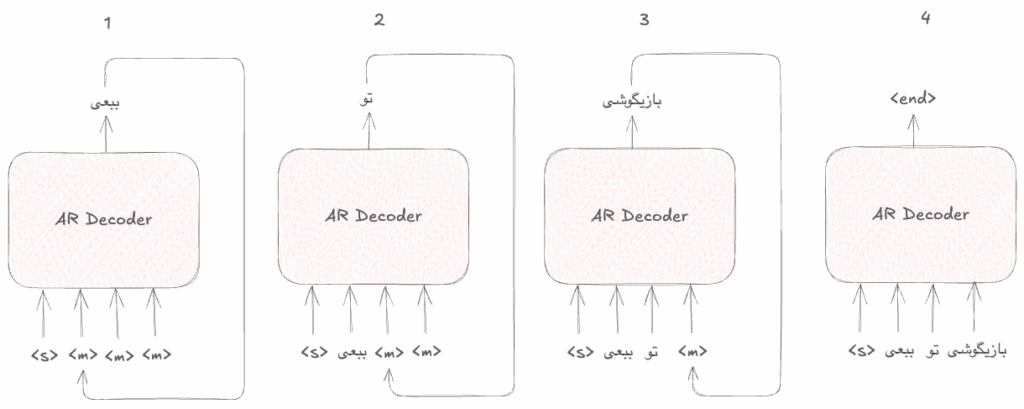
The current stack of decoding in LLMs
Transformers are the building block of LLMs despite all the improvements and changes that have been achieved in recent years. Transformers are made up of 2 main components: encoder and decoder. Most of the existing LLMs are only built using the decoder component, and that’s why they are sometimes referred to as decoder-only transformers.
The process of decoding in this approach is fully causal and auto-regressive. meaning that the decoder will start generating tokens strictly in a left-to-right manner and for generating the next token needs to digest all the previously generated tokens as well.
If you think about it, this actually makes sense and natural language is causal and choosing the next word depends on the previously picked words.
The following illustration shows what the process of decoding looks like in the transformers:
An introduction to diffusion and discrete diffusion
Before getting into the diffusion large language models, we need to have a basic understanding of what diffusion means and how it can be used for discrete structures like languages.
Continuous diffusion
Diffusion models were first introduced for image generation tasks, in which the model was trained to be able to generate an image from pure random Gaussian noise. The first impressive image generation models like DALL-E were based on diffusion generation as well.
In this approach, the goal is to train the model to learn how to de-noise any given data in a specific domain that it is trained on. To achieve this, we gradually add noise to the input image in T time-steps and then in the decoding process, teach the model to remove the noise while being aware of the timestep, so the model will try to guess and remove the noise that was added in a specific timestep to the image.
We can write this process using mathematics as well. For the forward nosing process we have:
$$ q(x_{1:T}|x_0) = \prod^{T}_{t=1}q(x_t|x_{t-1}) $$
This is describing the process of adding noise to the original x0 data over T time-steps in which each time-step is only directly depending on the previous time-step.
For the backward de-noising process, we need to calculate the joint probability of entire noising sequence from x0 to xT:
$$ p_{\Theta}(x_{0:T}) = p_{\Theta}(x_T)\prod^T_{t = 1} p_{\Theta}(x_{t-1} | x_t) $$
This backward process is parameterized and is learned during training.
This process can generate a valid sample that is close enough to the domain that the model was trained on, for example if the training dataset are all images of cars, by giving a pure noise to this model,it will generate an image of a car that doesn’t necessary exist in the training set, but is close enough to the ones that exist in it.
Discrete diffusion
Discrete diffusion is a little different from the normal diffusion, we have a discrete set of items that need to be masked in consecutive time-steps and then be unmasked to form a valid construct again, like building a sentence with a set of given words.
The general process is still the same, we have an input sequence that should be masked, and for masking we need to define a special masking token, and at each timestep, we randomly replace some tokens with the masking token.
To show the forward process using mathematical notations we have:
$$ q(x_t | x_{t-1}) = Cat(x_t;Q^T_t x_{t-1}) $$
Which is showing that the corrupted sequence of time-step t is based on the sequence in its previous step, and we’re using a transition matrix Q, to decide which tokens in the input sequence to be replaced by the masking token. The transition matrix itself is defined as following:
$$ Q_t = (1 – \beta_t)I + \beta_t1m^T $$
By increasing the value of beta at each timestep, more items in the sequence will be replaced by the mask token.
Diffusion large language models
Diffusion large language models are LLMs that follow the diffusion approach for generating their outputs. This means the model can behave non auto-regressive and generate tokens in different orders.
Despite the causal nature of languages, allowing the model to be non auto-regressive has the added benefit of increasing the speed of generation and completing the generation in fewer timesteps than are required for the full auto-regressive generation.
Diffusion models are also presumed to be able to do Global context planning that could improve the performance of the model in tasks like code generation.
Training dLLMs
To train an LLM, we can take an already trained LLM and gradually adapt it to perform the diffusion task, or we can just train a model from scratch to perform the diffusion.
Most of the existing dLLMs are following the adaptation path and are based on a well known LLM like Qwen.
The auto-regressive decoding step in LLMs only predicts a single next token which means the loss we try to minimize can be defined like this:
$$ L_{AR} = – \sum_{i = 0}^N log(x_i | x \leq i) $$
This loss function is focusing on only predicting a single token right, in the adaptation process, we start with a per-trained LLM, pick a dataset, mask the tokens in consecutive time steps and expect the model to un-mask the tokens, while being aware of the timestep. The model is expected to generate the correct tokens regardless of the position of the token in the sequence.
Models like Dream and DiffuCoder have a separate training phase after adaptation pre-training called annealing in which datasets with fewer tokens but with higher quality are used to improve the models capability on general tasks like speaking or generating code.
And finally we get to the instruction-tuning step where the model is taught to perform instructions like question-answering and be guided to generate answers that are compliant with human preferences.
This is a representation of the training process of DiffuCoder, a dLLM design specifically for code generation tasks.

Since language generation falls into the category of discrete diffusion, after each pass of diffusion decoding, we need to pick 1 or more of the predicted tokens with the highest probability and mask the rest of the predicted values again to be processed again.
Auto-regressiveness in dLLMs
Human language is inherently auto-regressive, meaning that picking a word in a sequence should change the probability of the next words that can be used to generate a correct sequence.
While being auto-regressive is not the desired outcome we expect in diffusion large language models, it is commonly observed that if models generate their responses semi-autoregressive (for example generating blocks of text in the left to right order) the generated response has a better quality.
To study the auto-regressiveness of a model we need to have a measure for it, and the measures of local and global AR-ness is introduced by the researchers of DiffuCoder.
- The local AR-ness is defined as: Consecutive next-token prediction pattern:
- For a sequence of length K, we measure how many of the generated tokens follow the pattern of next-token prediction. It is obvious that by increasing the length of the sequence, the local AR-ness will decay
- The global AR-ness is defined as: Earliest mask selection
- We specify a length of K in the sequence and count how many of the unmask tokens are falling into the range of those first K tokens. if we pick a bigger K, the global AR-ness will grow.
By specifying this metrics for AR-Ness we can study how the AR-Ness changes during the training stages and if the model shows different AR-Ness with different types of tasks (for example mathematics and coding).
The published results in the DiffuCoder paper is interesting as it points out that the model shows an increased amount of AR-Ness:
- after the annealing training phase and when exposed to higher quality data
- model has lower global AR-Ness when generating code compared to when answering mathematical questions, the model usually generates some of the late tokens first before unmasking the early tokens when generating code.
- The global AR-Ness has a minor fall after the RL training for preference alignment and instruction tuning.
dLLMs for code generation
One interesting aspect of using dLLMs for code generation is the concept of global planning in diffusion models, in contrast to the AR LLMs, dLLMs don’t have to start from a given point to generate the code, they can go back and forth between the functions and classes and even change some of the early tokens based on a token in one of the late positions given the bi-directional attention, which seems closer to how the process of coding is.
None of the existing dLLMs aren’t big enough to beat the commercial AR LLMs, but the comparisons between the small dLLMs and LLMs on coding benchmark datasets shows that there is hope for a new paradigm to dominate the architecture of LLMs in the near future.
Conclusion
- dLLMs are a relatively new approach for generating text that are inspired by the concept of discrete diffusion.
- They can to some level leave the traditional Auto-Regressive text generation of LLMs behind and generate texts starting from arbitrary positions in the final output.
- dLLMs can be used to generate texts with a much lower cost, since they can unmask multiple tokens at each pass and increase the generation speed by a factor of 2 and possibly even more.
- Given that dLLMs can have bi-directional attention and global planning during the decoding phase, tokens generated at a late position can affect and change the tokens that should be generated at earlier positions which seems to be more useful for code generation tasks.